こんにちは、よっさんです。今日はバランサーについて簡単に説明したいと思います。factorioで使用するバランサー、調べれば使いたいバランサーの情報やブループリントがあると思いますが、どういう仕組みになっているのかの説明がないものもあります。やみくもにブループリントを使っていても原理を知っておきたいという方のために、factorioでよく使うバランサーの紹介と、その仕組みについて紹介したいと思います。
1-6 バランサー
factorioで私が一番初めに使用したバランサーです。このような形状になります。

動作としては入力(黄色い矢印のところ)から入った部材を出力(青の矢印のところ)に均等に1/6に割り当てます。
使用場所・メリット
列車の荷物を積むところです。貨物車両には片方に6列分の荷物の積み下ろしをするスペースがあります。採掘場で次の列車が到着するまでの間に、荷物を均等に最大までチェストに保管します。

このバランサーを用意しないと、チェストの保管量にばらつきが発生します。そうすると、貯まっていないチェストは空になるとずっと動かず待機します。逆に一番貯まったチェストから細々と積み込みが発生します。よく列車の発車条件に”積荷が満杯”とか”インサータの動作が停止してX秒経過”とか設定して駅の待機時間を短くする工夫をすると思いますが、それが結果非効率になります。
仕組み・計算
このバランサーを初めて見たとき、右上のフィードバックの部分が意味不明でした。本当に均等に割り当ててくれるのか、、、というわけで考えてみましょう。
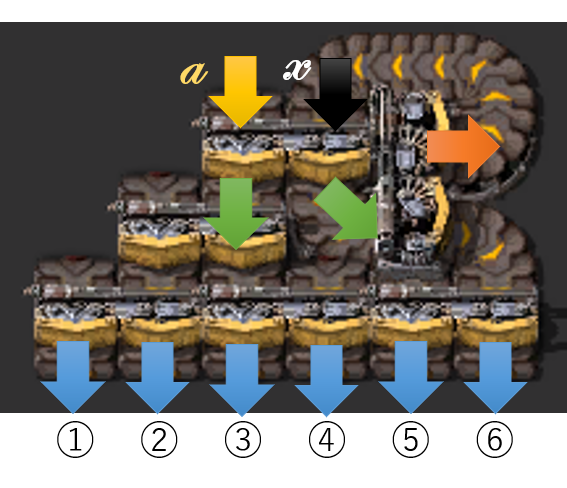
まずは、黄色の矢印の搬送量を\(a\)と置きます。次にこのフィードバックの部分、黒の矢印です。ここはよくわからないのでここをひとまず\(x\)と置きます。そうすると、1段目の分配器の出力(緑の矢印)は、平均化されるため、
\((a + x) / 2\)
と置けます。
次に右側の分配器の出力(橙の矢印)です。ここはこの緑の矢印を半分に分配することになるので、
\((a + x) / 4\)
となります。ここで出力の片方を1段目の入力に戻していますね。よって、黒と橙の矢印がつながるので下記の方程式が成り立ちます。
\( x=(a+x)/4 \)
→ \(4x=a+x\)
→ \(3x=a\)
→ \(x=\frac{1}{3}a\)
ここで、\(x\) が \(a\) の 1/3であることがわかりました。簡単な方程式ですが、果たして本当に6分配されるのでしょうか?ここで緑の矢印から\(x\)を削除します。
\((a + x ) / 2 = (a + \frac{1}{3}a) / 2 \)
\( =(\frac{4}{3}a) / 2 = \frac{2}{3} a \)
青の矢印の①から④はこの緑の矢印を4分配していますね?つまり、
\(\frac{2}{3} a \times \frac{1}{4} = \frac{1}{6} a \)
となります。では残りの⑤と⑥ですが、これは橙の矢印を2分配しています。つまり、
\({(a + x ) / 4} / 2 = {(a + \frac{1}{3}a) / 4} / 2 \)
\(= \frac{4}{3}a / 4 / 2 = \frac{1}{3} a / 2 \)
\( =\frac{1}{6} a \)
これですべての矢印が \(\frac{1}{6}\)となり、均等に割りあたっていることがわかりました。
3-3バランサー
本当に有名なのは4-4バランサーなのですが、これは本当によく見かけるので3-3バランサーを解説します。このような形状をしています。

使う場所・メリット
メインバスで流動する部品の中には、「いや、これは4列はいらないだろ」というような部品もあります。例えば、鋼鉄とかプラスチック、赤基板とかでしょうか。
仕組み・計算
これも同じようにそれぞれのラインに矢印を付けて見ていきます。

まずは入力が3つあります。これの流量をそれぞれ\(a, b, c\)とします。バランサーの目的は、出力のすべてのラインに対して\((a+b+c)/3\)に分配することです。またフィードバックが出てきました。これはxと置きましょう。
左の1段目の分配器の出力(青の矢印)は\(a\)と\(b\)の平均なので、
\((a+b)/2\)
となります。次に右の1段目の分配器の出力(紫の矢印)は\(c\)と\(x\)の平均なので、
\((c+x)/2\)
となります。では2段目の分配器の出力はどうでしょう。これは青と紫の矢印の平均なので、
\(\{(a+b)/2 + (c+x)/2\}/2 \)
\( = (a+b+c+x) /4\)
となります。ここで片方の出力がフィードバックされるため、赤と橙の矢印が繋がりました。ここで方程式を立てて、\(x\)について解くと、
\(x = (a+b+c+x) /4 \)
→ \(4x = a+b+c+x \)
→ \(3x = a+b+c \)
→ \(x = (a+b+c)/3 \)
と求まります。ここから、出力がどうなるのかを見ていきます。ここで一番左の出力ですが、この橙の矢印がそのまま出力されています。つまり、\(x\)の値がそのまま出力されていますのでこの出力は\((a+b+c)/3\)と正しく分配がされていることがわかります。
残りの2つの出力ですが、これは青と紫の矢印の平均です。→ さっき求めた橙の矢印ですね。つまり、ここも\((a+b+c)/3\)と正しく分配されていることがわかります。
以上からすべての出力が等しく3分割されていることがわかるかと思います。



